Swiss Table#
一种专门的哈希表实现,用于动态地将键字段值的组合映射到一组紧凑的整数ID。ID 之后可以代替键来识别具有相同键的行组。
介绍#
Arrow 中的哈希分组使用基于称为 Swiss table 的数据结构的哈希表变体。Swiss table 使用线性探测。有一个槽数组,插入的键相关的信息存储在这些槽中。哈希函数确定在哈希表查找期间开始搜索匹配键的槽。然后,槽按顺序访问,在数组末尾环绕,直到找到匹配或空槽,后一种情况意味着没有匹配。Swiss table 将槽组织成8个块,其设计支持块级别的数据级并行性。更准确地说,它允许在查找期间通过简单的64位算术同时访问块中的所有槽。SIMD指令可以进一步增强这种数据级并行性,允许使用64位元素的SIMD向量同时处理与多个输入键相关的多个块。块中被占用的槽总是聚集在一起。Swiss table 的名称来自于将生成的空槽序列比作一维奶酪中的孔。
接口#
用于实现连接和分组操作的查询处理中的哈希表不需要提供通用哈希表的所有操作。简化的要求可以帮助实现更简单、更高效的设计。例如,我们不需要能够删除以前插入的键。它是一个只附加的数据结构:可以添加新键,但从不删除旧键。此外,每个键只能插入一个副本——从这个意义上说,它类似于 std::map 而不是 std::multimap。
我们的 Swiss table 是完全向量化的。这意味着所有方法都处理输入键向量,分批处理它们。通常会为性能关键操作提供专门的 SIMD 处理函数实现。核心哈希表代码中使用的所有回调接口也设计为处理批处理输入而不是单个键。批处理大小几乎可以是任意的,由哈希表的客户端选择。批处理大小应该是最小的输入项数量,足够大,以便充分体验向量化和 SIMD 的好处。保持小意味着用于存储计算中间结果的临时数组(堆栈上保留的一些临时变量的向量等效物)使用的内存更少。这反过来意味着 CPU 缓存中的空间更小,这也意味着对其他内存访问密集型操作的影响更小。我们将1024作为批处理的默认大小。我们将其称为迷你批处理,以区别于代码中更高层次使用的其他形式的批处理,例如在为工作线程或分析查询中的关系运算符调度工作时。
Swiss table 的主要功能是将任意复杂的键映射到唯一的整数 ID。我们称之为查找或插入。给定一个键值序列,返回一个相应的整数 ID 序列,使得所有相等的键都接收相同的 ID,并且对于 K 个不同的键,整数 ID 将从数字0到(K-1)的集合中分配。如果我们在哈希表中找到给定输入的匹配键,我们返回首次将键插入哈希表时分配的键 ID。如果未能找到已插入的匹配项,我们将第一个未使用的整数分配为键 ID,并向哈希表添加一个新条目。由于向量化处理可能导致单个输入的乱序处理,因此不能保证如果同一输入批处理中有两个新键值,并且其中一个在输入序列中出现得更早,则它将收到更小的键 ID。可以在基本映射到整数键 ID 的基础上构建额外的映射功能,例如,如果我们想为所有唯一键分配并可能继续更新一些值,我们可以将这些值保存在按获得的键 ID 索引的可调整大小的向量中。
Swiss table 的实现不需要与键域相关的任何信息。它不使用它们的逻辑数据类型或关于它们的物理表示的信息,甚至不使用指向键的指针。对键的所有访问都委托给一个或多个单独的类,这些类提供三个操作的回调函数
计算键的哈希值;
检查给定键对的相等性;
将给定键序列附加到 Swiss table 对象外部维护的堆栈,以便之后可以通过键 ID 引用它们(键 ID 将等于它们在堆栈中的位置)。
将参数传递给回调函数时,键使用整数 ID 引用。对于左侧——即输入迷你批处理中存在的键——使用该迷你批处理中的序数位置。对于右侧——即插入到哈希表中的键——它们通过首次遇到和处理时分配并存储在 Swiss table 中的键 ID 来标识。
回调中信息传递的逻辑视图图
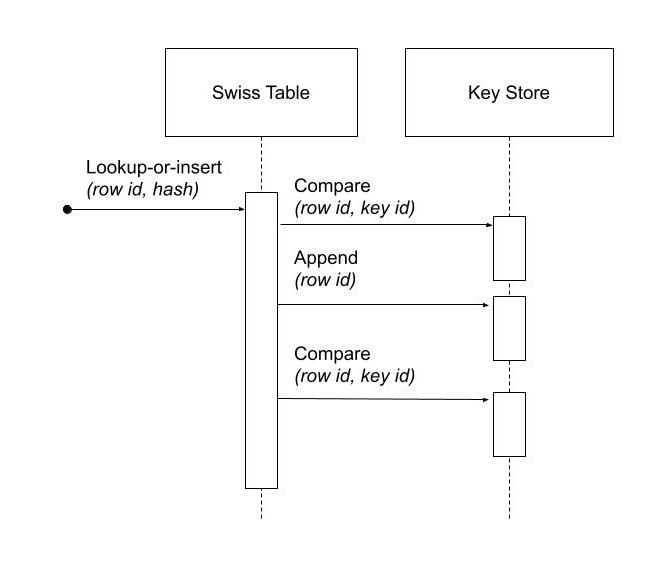
插入键的哈希表值也存储在 Swiss table 中。因此,哈希表逻辑不需要重新评估哈希,实际上也不需要哈希函数回调。调用查找或插入时,调用者为批处理中的所有条目提供哈希值就足够了。
基本架构和数据组织#
哈希表是槽的数组。槽被分组为8个一组,称为块。块的数量是2的幂。空的哈希表从一个块开始,所有槽都为空。然后,随着键的插入和空槽数量的减少,在某个时刻会触发哈希表的大小调整。存储在槽中的数据将移动到一个新的哈希表,该哈希表的块数量是原来的两倍。
下图显示了我们实现的 Swiss table 中数据的基本组织
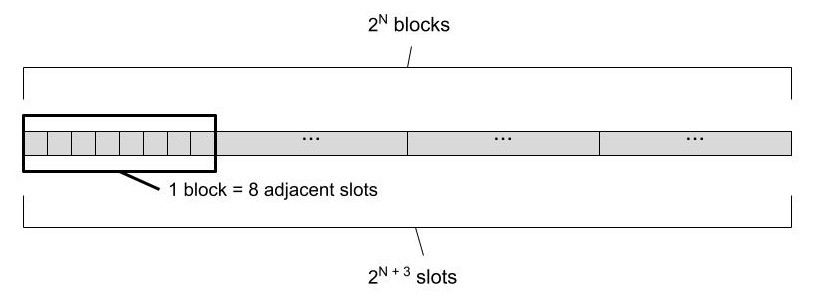
N 是块数的对数,\(2^{N+3}\) 是槽数,也是最大插入键数,因此 (N + 3) 是存储键 ID 所需的位数。我们将 N 称为哈希表的大小。
数组中块的索引将称为块 ID,类似地,槽的索引将是槽 ID。有时我们将关注单个块,并通过使用局部槽 ID(索引从0到7)来指代属于它的槽。
每个槽都可以是空的或存储与单个插入键相关的数据。槽中存储了三条信息
状态字节,
键 ID,
键哈希值。
顾名思义,状态字节存储8位。最高位表示槽是否为空(最高位设置为1)或对应于已插入的键之一(最高位为0)。剩余的7位包含键哈希值的7位,我们称之为印记。印记用于在搜索给定输入的匹配键时消除一些假阳性。槽还存储键 ID,它是一个非负整数,小于已插入键的数量,用作对实际插入键的引用。与插入键相关的最后一条信息是它的哈希值。我们存储所有键的哈希值,这样就不需要重新计算它们。这极大地简化了一些操作,例如哈希表的大小调整,甚至可能根本不需要查看键。对于空槽,状态字节为 0x80,键 ID 为零,哈希值不使用,可以设置为任意数字。
一个块包含8个槽,可以看作是一个最多可容纳8个插入键的微堆栈。当第一个键插入到空块中时,它将占用局部 ID 为0的槽。第二个插入键将进入槽号1,依此类推。我们使用哈希值的 N 个最高位来获取起始块的索引,当搜索匹配或用于插入以前未见过的键的空槽时。如果起始块包含任何空槽,那么搜索匹配或插入键的位置将在该块结束。我们将这样的块称为开放块。未开放的块是满块。在满块的情况下,输入键相关的搜索可能会在下一个块中继续,取模于块数。如果键未插入到其起始块中,我们将将其称为溢出条目,其他条目为非溢出条目。溢出条目处理速度较慢,因为它们需要访问多个块,因此我们希望将它们的百分比保持在较低水平。这通过选择正确的负载因子(哈希表中被占用的槽的百分比)来完成,在该负载因子下,哈希表会调整大小,块数会加倍。通过调整此值,我们可以控制遇到溢出条目的概率。
每个块中最有趣的部分是其槽的状态字节集,它只是一个64位字。在查找期间在这些字节中进行高效搜索的实现需要使用前导零计数或尾随零计数内联函数。由于在某些情况下只有第一个可用,为了利用它,我们将64位状态字中的字节排序,使得块中的第一个槽使用最高字节,最后一个槽使用最低字节(槽按字节顺序反转)。下图显示了槽信息如何存储在64位状态字中
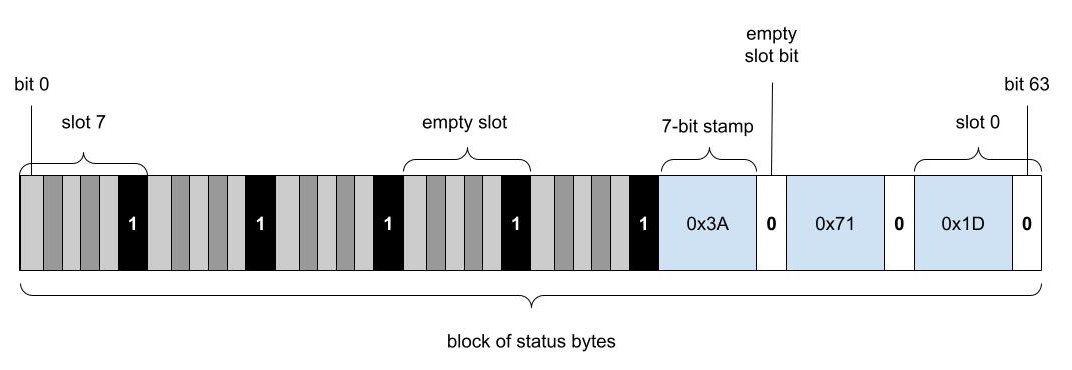
每个状态字节都有一个哈希值的7位片段——一个印记——和一个空槽位。空槽的状态字节等于0x80——最高位设置为1表示空槽,最低位(用于印记)设置为零。
下图显示了哈希表使用了哈希值的哪些位
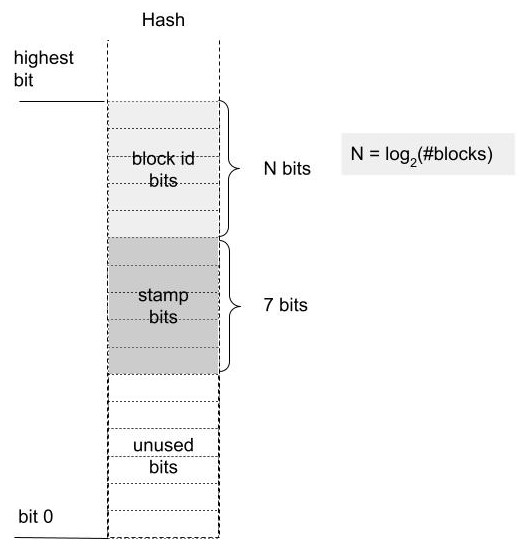
如果哈希表有 \(2^{N}\) 个块,那么我们使用哈希值的 N 个最高位来选择起始块以搜索匹配。接下来的7位用作印记。使用最高位来选择起始块意味着哈希值范围可以轻松映射到该范围内哈希值的起始块的块 ID 范围。这在调整哈希表大小或合并两个哈希表时非常有用。
状态字节和键 ID 的交错#
所有槽的状态字节和键 ID 都存储在一个字节数组中。它们首先按8个一组分组,然后每个状态字节块与相应的键 ID 块交错。最后,键 ID 使用尽可能少的位数表示并进行位打包(表示每个下一个键 ID 的位紧接在前面键 ID 的最后一位之后开始)。请注意,无论选择的位数如何,一个位打包的键 ID 块(即8个)都将以字节边界开始和结束。
下图显示了交错数组中单个块的字节和位的组织
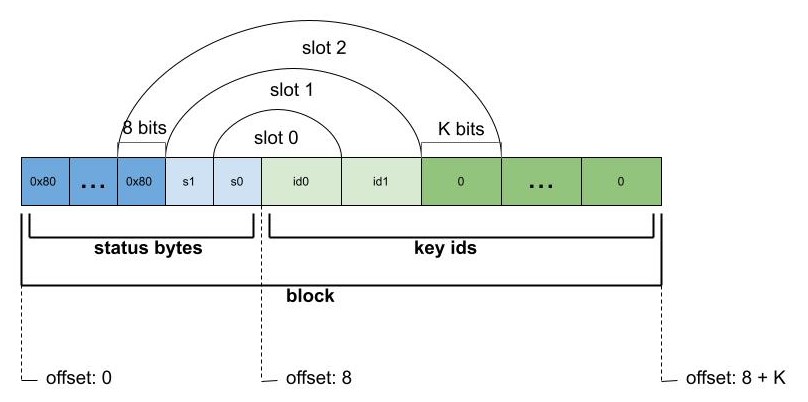
从哈希表的大小我们可以推导出在最坏情况下编码任何键 ID 所需的 K 位数。K 等于表示槽 ID 所需的位数(键数不大于槽数,任何键 ID 都严格小于键数),对于大小为 N(N 个块)的哈希表,K 等于 (N+3)。为了简化位打包和解包并避免处理特殊情况,我们将 K 向上取整到完整的字节,如果 K > 24 位。
状态字节以反向字节顺序(最后一个字节对应于局部 ID 为0的槽)存储在一个64位字中。另一方面,键 ID 以正常顺序(槽 ID 的顺序)存储。
由于给定槽的状态字节和键 ID 都存储在同一个数组中,彼此靠近,我们可以预期大多数查找只会从 Swiss table 代码内部从内存中读取一个 CPU 缓存行(然后至少在 Swiss table 外部再读取一个以访问用于比较的键的字节)。即使我们遇到溢出条目,它仍然可能与起始块数据位于相同的缓存行上。哈希值与状态字节和键 ID 分开存储,仅在调整大小时使用,并且不影响这些事件之外的查找。
注意
需要考虑的改进:除了 Swiss table 数据,我们还需要存储一个已插入键的数组,每个键 ID 对应一个。如果键是固定长度的,那么键字节的地址可以通过将键 ID 乘以键的公共长度来计算。如果键的长度可变,那么将有一个额外的数组,其中包含每个键在连接的键字节数组中的偏移量。这意味着查找过程中的任何键比较都将涉及3个数组:一个用于获取键 ID,一个用于获取键偏移量,最后一个用于键的字节。如果我们将键偏移量而不是键 ID 与槽状态字节交错存储,则可以减少到2个数组查找。由键 ID 索引并存储在其自身数组中的偏移量变为由槽 ID 索引并与槽状态字节交错存储的偏移量。同时,之前由槽 ID 索引并与槽状态字节交错存储的键 ID 变为使用偏移量引用并与键字节一起存储的键 ID。哈希表所需的总内存大小可能会略有增加,增加量等于用于存储偏移量和用于存储键 ID 的位数之差乘以槽数,但这应该是总大小的一小部分。
32位哈希与64位哈希#
目前我们在 Swiss table 代码中使用32位哈希值,并使用32位整数作为键 ID。对于健壮的实现,迟早我们需要支持64位哈希和64位键 ID。当我们使用32位哈希时,这意味着当哈希表大小 N 大于25时(选择块需要25位哈希,生成印记字节需要7位,总计32位),哈希位就会耗尽。当插入的键数超过大小为25的哈希表中存储的最大键数(至少为 \(2^{24}\))时,查找期间出现假阳性的几率将迅速增加。32位哈希不应与超过约1600万个插入键一起使用。
低内存占用和低哈希冲突几率#
Swiss table 是现代硬件哈希表的良好选择,因为它将可以利用特殊 CPU 指令的查找与空间效率和低哈希冲突几率结合在一起。
空间效率对性能很重要,因为随机数组访问的成本(通常在较大的哈希表中主导查找成本)随着数组的大小而增加。这是由于 CPU 缓存空间有限造成的。让我们看看除了存储所有这些键数据的基本成本之外,哈希表中键的摊销额外存储成本是多少。此外,我们可以跳过哈希值的存储,因为它们仅在不频繁的哈希表大小调整操作中使用(在正常情况下不应对 CPU 缓存使用产生重大影响)。
大小为 N 的半满哈希表将为每个插入的键使用2个状态字节(因为每个填充的槽都有一个空槽)和2*(N+3)位用于键 ID(同样,一个用于已占用的槽,一个用于空的)。例如,对于 N = 16,这略低于每个插入键7字节。
Swiss table 的误报概率也很低,从而导致浪费的键比较。这里有一些为什么会这样的理由。大小为 N 的哈希表最多可以包含 \(2^{N+3}\) 个键。搜索匹配涉及 (N + 7) 个哈希位:N 用于选择起始块,7 用于作为印记。哈希表中使用的哈希位组合总是至少比键数多16倍(如果哈希表半满,则多32倍)。这些数字意味着搜索匹配槽导致的误报概率应该很低。这对应于对于已存在的键,每次查找的预期比较次数接近1,对于新键则接近0。
查找#
查找或插入操作,给定键的哈希值,找到可能与输入键相等的候选槽列表及其对应的键。该列表可能为空,这意味着键尚不存在于哈希表中。如果它不为空,则对每个下一个候选调用键比较回调函数以验证确实存在匹配。假阳性被拒绝,我们最终要么找到实际匹配,要么找到空槽,这意味着该键是哈希表的新键。新键被分配下一个可用的整数作为键 ID,并附加到存储在哈希表中的键集合中。由于将新键插入哈希表,已占用槽的密度可能达到上限,此时哈希表将调整大小,之后槽数将增加一倍。这是查找或插入功能的总结,但实际实现由于处理的向量化和常见情况的各种优化而稍微复杂一些。
单个块内的搜索#
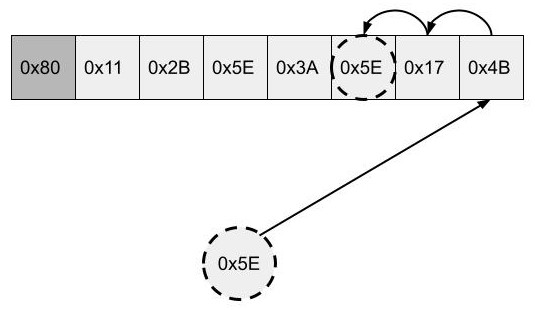
在单个块内搜索给定键的匹配(即,给定键的印记)时,可能发生三种情况,如下所示。
状态字节块中存在匹配的印记
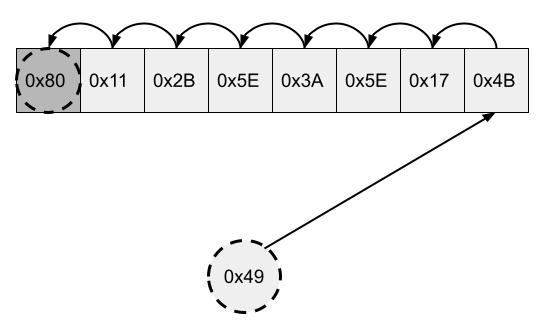
块中没有匹配的印记,但块中有一个空槽
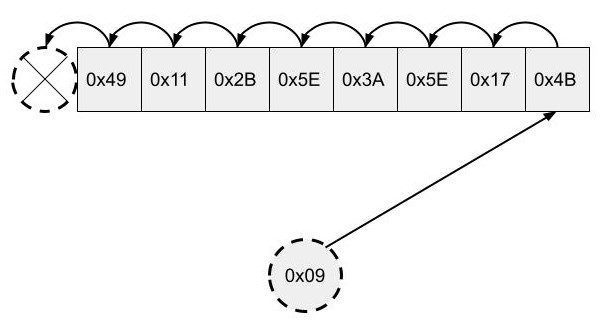
块中没有匹配的印记,并且块已满(没有剩余空槽)
可以使用64位算术同时在整个单个块中搜索匹配的槽,而无需遍历其中的所有槽。下面是查找给定印记的第一个状态字节的步骤序列示例,如果块未满,则在未命中时返回第一个空槽,否则返回8(超过最大局部槽 ID)。
以下是搜索单个块中匹配印记时可能执行的步骤草图。
[1条指令] 将印记复制到所有字节,乘以 0x 0101 0101 0101 0101。
我们得到:0x 5E5E 5E5E 5E5E 5E5E。[1条指令] 将复制的印记与状态字节字进行异或操作。对应匹配印记的字节将为0,对应空槽的字节值介于128到255之间,对应不匹配非空槽的字节值介于1到127之间。
我们得到:0x 1549 0064 0075 4FDE。[2条指令] 在下一步中,我们希望在每个字节的最高位中获得有关匹配的信息。我们可以忽略空槽字节,因为它们将在稍后的步骤中处理。设置每个字节的最高位(与 0x 8080 8080 8080 8080 进行或运算),然后从每个字节中减去1(从64位字中减去 0x 0101 0101 0101 0101)。现在,如果一个字节对应于非空槽,则最高位0表示匹配,1表示未命中。
我们得到:0x 95C9 80E4 80F5 CFDE,然后 0x 94C8 7FE3 7FF4 CEDD。[3条指令] 在下一步中,我们希望在每个字节中获得两个值之一:如果是空槽或匹配,则为 0x80,否则为 0x00。我们分三步完成:对上一步的结果进行非运算,以改变最高位的含义;与原始状态字进行或运算,以将空槽的字节中的最高位设置为1;屏蔽掉所有字节中除最高位以外的所有内容(与 0x 8080 8080 8080 8080 进行与运算)。
我们得到:6B37 801C 800B 3122,然后 6B37 DE3E DE2B 31A2,最后 0x0000 8000 8000 0080。[2条指令] 最后,使用前导零位计数并将其除以8,以找到对应于匹配或空槽的最后一个字节的索引。如果前导零计数内在函数对于64位输入零返回64,那么在除以8之后,在块已满且没有任何匹配的情况下,我们也将得到所需的结果。
我们得到:16,然后 2(块中与印记匹配的第一个槽的索引)。
如果 SIMD 指令具有64位通道,则可以同时执行多个针对不同键的单块搜索。例如,AVX2 指令集允许在一条指令中处理四组64位值,即同时进行四次搜索。
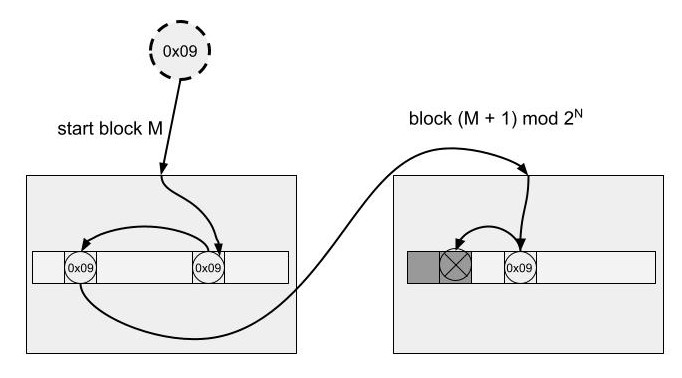
潜在跨多个块的完整搜索#
搜索匹配键的完整实现可能涉及访问多个块,从根据键的哈希值选择的起始块开始。当我们在当前块中找不到匹配且当前块已满时,我们会移动到下一个块(取模于块数)。搜索还可能涉及访问每个块中的一个或多个槽。在这种情况下,访问意味着在遇到具有匹配印记的槽时调用比较回调以验证匹配。最终搜索停止,当满足以下任一条件时
在与印记匹配的槽中找到匹配的键,或
到达一个空槽。如下图所示
两阶段的乐观处理#
在悲观情况下,哈希表查找的成本可能很高,当我们遇到哈希冲突和导致访问更多块的满块时。在大多数情况下,我们可以预期乐观情况——起始块不满,因此我们只会访问这个块,并且块中的所有印记都不同,因此我们最多只需要一次比较即可找到匹配。我们可以预期大约90%的现有键查找会通过乐观处理路径。因此,专门优化这90%的输入是值得的。
Swiss table 中的查找分为两遍遍历输入键批处理。第一遍:快路径查找,是一种高度优化、向量化、SIMD友好、无分支的代码,完全处理乐观情况。第二遍:慢路径查找,通常只针对第一遍中未完成的输入选择执行,尽管它也可以直接在所有输入上调用,跳过快路径查找。它处理所有特殊情况和插入,但为了健壮性,它不如快路径高效。慢路径查找不需要重复快路径查找中完成的工作——它可以将快路径查找结束时达到的状态作为起点。
快路径查找仅在起始块中搜索第一个印记匹配。它仅在我们已将至少一个键插入到哈希表中时才有意义,因为它不处理插入。它将键哈希向量作为输入,并根据它为每个键输出三条信息
与找到匹配印记的槽对应的键 ID。如果未找到匹配印记,则为任何有效的键 ID。
一个标志,指示是否找到匹配。
如果第一个匹配未找到或在评估键比较后发现是假阳性,则慢路径应从哪个槽 ID 开始搜索。
注意
需要考虑的改进:预计算第一遍查找结果。
如果哈希表很小,插入的键数量很少,我们可以通过在查找表中存储所有哈希位组合的预计算结果来进一步简化和加速第一遍。让我们考虑大小为5的 Swiss table,它有256个槽,最多可以插入128个键。在这种情况下,查找只使用12位哈希:5位选择一个块,7位创建一个印记。对于所有 \(2^{12}\) 种位组合,我们可以在一个数组中保存第一遍查找的结果。键 ID 和匹配指示标志可以使用一个字节:7位用于键 ID,1位用于标志。请注意,槽 ID 仅在我们进入第二遍查找时才需要,因此它可以单独存储,并且可能只被一小部分键访问。快路径查找几乎变成从一个4KB数组中获取结果的单次操作。用于实现此功能的查找数组需要与槽数据的主副本保持同步,这在插入期间需要额外注意。由于查找数组中的条目数量远高于槽数量,因此此技术仅适用于小型哈希表。
密集比较#
如果哈希表中至少插入了一个键,那么每个槽都包含一个键 ID 值,该值对应于某个实际键,可用于比较。这是因为空槽的键 ID 初始化为0。在快路径查找之后,我们得到每个输入的匹配找到标志。如果它已设置,那么我们需要将输入键与哈希表中由快路径代码返回的键 ID 标识的键进行比较。比较将验证键之间是否存在真正的匹配。我们只需要对具有匹配候选的输入子集执行此操作,但由于我们所有输入都有对应真实键的键 ID 值,我们也可以无条件地对所有输入执行比较。如果大多数(例如,超过80%)的键具有匹配候选,那么对剩余部分键进行比较而不进行过滤的成本实际上可能比仅对所需键进行评估同时引用过滤信息的成本更低。这可以看作是用于避免代码中发散条件分支的通用预处理技术的一种变体。它可以根据某种启发式方法用于验证快路径查找报告的匹配,并被称为密集比较。
调整大小#
新的哈希表初始化为空,只有一个块,只能容纳少量键条目。随着更多键的插入,哈希表大小加倍变得必要。它在查找的第二遍中调用,这也处理插入。它发生在插入键的数量达到根据哈希表当前大小确定的特定上限之后立即发生。调整大小后,输入迷你批处理中可能仍有未处理的条目,因此查找的第二遍会立即重新启动,使用更大的哈希表和剩余的未处理条目子集。
目前的策略,应该相当有效,是当小型哈希表(最大8KB)达到50%满时调整其大小。大型哈希表在75%满时调整大小。我们希望内存中的大小尽可能小,同时保持块变满的低概率。
在讨论调整大小时,我们将讨论调整大小源和调整大小目标表。下图显示了源表和目标表如何对相同的哈希位进行不同的解释。
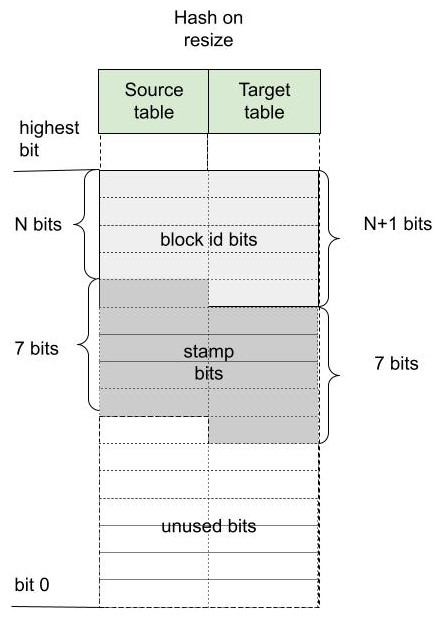
对于给定的哈希值,如果起始块 ID 在源表中为 L,则在目标表中它将为 (2*L+0) 或 (2*L+1)。基于此,我们可以在表之间迁移数据时期望数据访问局部性。
调整大小也很划算,因为哈希表中键的哈希值与其它槽数据一起保存,无需重新计算。这意味着调整大小过程不需要访问键的实际字节。
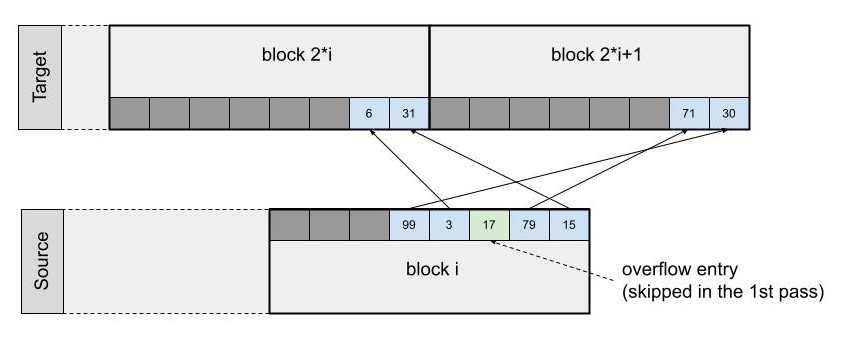
第一遍#
根据给定槽的哈希值,我们可以判断该槽是包含溢出条目还是非溢出条目。在第一遍中,我们按顺序遍历所有源槽,过滤掉溢出条目,并将所有其他条目移动到目标表。来自块 L 的非溢出条目将分布在目标表的块 (2*L+0) 和 (2*L+1) 之间。这些目标块都不会溢出,因为它们在此遍中最多只能容纳8个输入条目。
对于每个非溢出条目,源槽中印记的最高位决定了它将进入左侧还是右侧目标块。此外,可以避免此分区代码中的任何条件分支,以便结果有利于 CPU 执行管道。
第二遍#
在调整大小的第二遍中,我们再次扫描所有源槽,这次只关注在第一遍中跳过的溢出条目。我们只需使用通用插入代码将它们重新插入到目标表中,但有一个例外。由于我们知道所有源键都不同,因此无需搜索匹配的印记或运行键比较(或查看键值)。我们只需要找到目标表中从起始块开始的第一个开放块,并将其第一个空槽用作插入目标。
我们预计溢出条目很少见,因此该阶段的相对成本应该保持较低。

